何戦くらいなら実際にデータとして参考になるのか?
とりあえず勝率に限って話をしてみる。
無限に戦い続けた末の「本当の勝率」みたいなものがあるとする。
「本当の勝率からの誤差」と戦闘数との関係は、
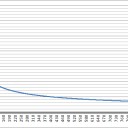
(↓95.44%ただしい: 2σ)
10戦 ±31.62%
50戦 ±14.14%
100戦 ±10.00%
200戦 ±7.07%
500戦 ±4.47%
1000戦 ±3.16%
10000戦 ±1.00%
95.44%正しいってのは、
「今の勝率」が95.44%の確率で上の誤差範囲に収まっているという意味。4.56%の確率で誤差範囲よりさらに外側。
にしても案外でかいっぽい。大まかな傾向をみるだけなら4~50戦、あれこれ議論するなら最低100戦くらいですかね?
ちなみに68.26%くらい正しい範囲(1σ)なら、誤差範囲は上の半分。99.74%くらい正しい範囲(3σ)は上の1.5倍。二項分布の標準偏差。
とりあえず勝率に限って話をしてみる。
無限に戦い続けた末の「本当の勝率」みたいなものがあるとする。
「本当の勝率からの誤差」と戦闘数との関係は、
(↓95.44%ただしい: 2σ)
10戦 ±31.62%
50戦 ±14.14%
100戦 ±10.00%
200戦 ±7.07%
500戦 ±4.47%
1000戦 ±3.16%
10000戦 ±1.00%
95.44%正しいってのは、
「今の勝率」が95.44%の確率で上の誤差範囲に収まっているという意味。4.56%の確率で誤差範囲よりさらに外側。
にしても案外でかいっぽい。大まかな傾向をみるだけなら4~50戦、あれこれ議論するなら最低100戦くらいですかね?
ちなみに68.26%くらい正しい範囲(1σ)なら、誤差範囲は上の半分。99.74%くらい正しい範囲(3σ)は上の1.5倍。二項分布の標準偏差。

コメント